前言

自从Transformer[3]模型在NLP领域问世后，基于Transformer的深度学习模型性能逐渐在NLP和CV领域(Vision Transformer)取得了令人惊叹的提升。本文的主要目的是介绍经典Transformer模型和Vision Transformer的技术细节及基本原理，以方便读者在CV领域了解和使用Vision Transformer。由于篇幅过长，本文将分为四个部分进行介绍，包括：

（1）自注意力与多头自注意力模型的原理与实现。

（2）Transformer的整体架构与实现。

（3）位置编码（positional encoding）的原理与实现。

（4）Transformer在CV领域的应用案例。

本文首先讲解第一个话题：自注意力（self-attention）与多头自注意力（multi-heads self-attention）模型的原理与实现。

注意力机制的直观认知

自注意力最早在自然语言处理领域提出，在Transformer[3]中，自注意力模型可以认为在学习一种关系，即一个序列中当前token与其他token之间的联系。

NLP领域

以一个自然语言处理中的序列翻译问题为例，直观地理解自注意力模型是如何发挥作用的，如下图所示。

自注意力机制效果图[1][3]。

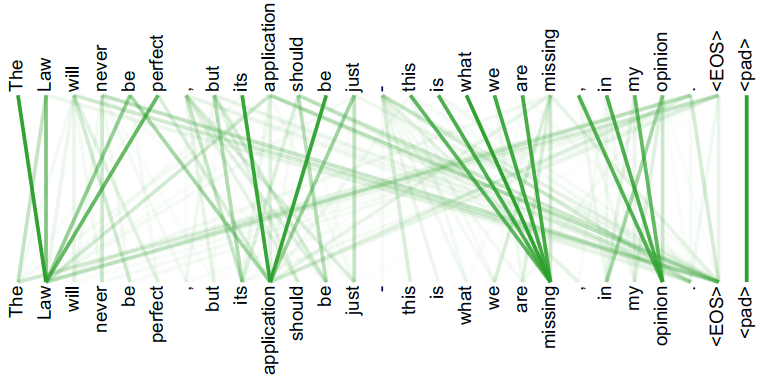
左侧效果图显示了一句话中单词it与其他单词的联系。可以发现，通过自注意力机制，Transformer模型建立起了单词it和所有其他单词的联系(橙色线条表示这种联系的权重，颜色越深表示联系越紧密)。并且，随着模型不断训练，我们发现it和The animal的联系最为密切，这正是我们想要获得的结果。通过这个例子可以看出，注意力机制有助于深度学习模型更好地理解文字序列中的每个token（单词）。

右侧效果图显示了一句话中任何一个token与其他所有tokens的联系，并且以连接线颜色的深浅表示这种联系的紧密程度。

CV领域

基于上述自注意力机制，早在Vision Transformer之前，就有很多基于注意力机制的深度学习模型，如经典的spacial attention、channel attention、CBAM等，其核心思想是自适应地提升特征表达在空间维度或（和）通道维度对特定位置的权重，增加神经网络对特定区域的关注程度。

以channel attention为例，可以看到channel attention模型通过重新分配特征图通道的权重，使模型更加关注某些通道，如下图所示。

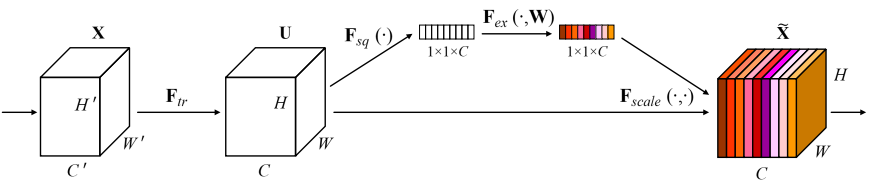
Squeeze-and-Excitation block (channel attention) [5]。Channel attention首先采用global average pooling将维度为[H, W, C]的特征图转化为[1, 1, C]，然后通过一个全连接层，最后将全连接层的输出结果与原始特征图相乘，在通道维度对原始特征图进行加权。这样，channel attention模型可在通道维度增加对某些通道的注意力，同时削弱对其余通道的注意力。

通过直观感受自注意力在不同领域发挥的作用，我们基本可以理解自注意力到底做了什么，并定性感受了为什么自注意力能够促进模型提升性能。后面，我们还将通过一些实际例子，发现自注意力机制在NLP和CV领域的一些联系，非常有意思。

自注意力

本节从自注意力的基本原理出发，首先通过一个序列翻译的例子讲解自注意力模型的计算过程及基本原理；然后，介绍自注意力模型的矩阵表达，以提升计算效率；接下来，将矩阵表达的过程整理为数学表达；最后，通过代码介绍自注意力模型的实现过程。

自注意力的过程和基本原理

整个自注意力的计算过程可以分为6个步骤。接下来逐步介绍每个步骤的操作过程和及其设计原理。

第一步：创建Query (q), Key (k)和Value (v)向量。 通过下图可以看到，对于输入tokens (单词) Thinking和Machines，首先采用Embedding算法将单词编码为词向量$X_1$和$X_2$；然后，对于每个词向量$X_i$，计算该词向量对应的Query, Key和Value，分别得到$q_1$, $k_1$, $v1$和$q_2$, $k_2$, $v_2$。需要注意的是，这里的$q_i$，$k_i$和$v_i$都是学习得到的，通过对应的输入向量$X_i$乘以对应的权重矩阵$W$ (即输入词向量通过一个全连接层)。

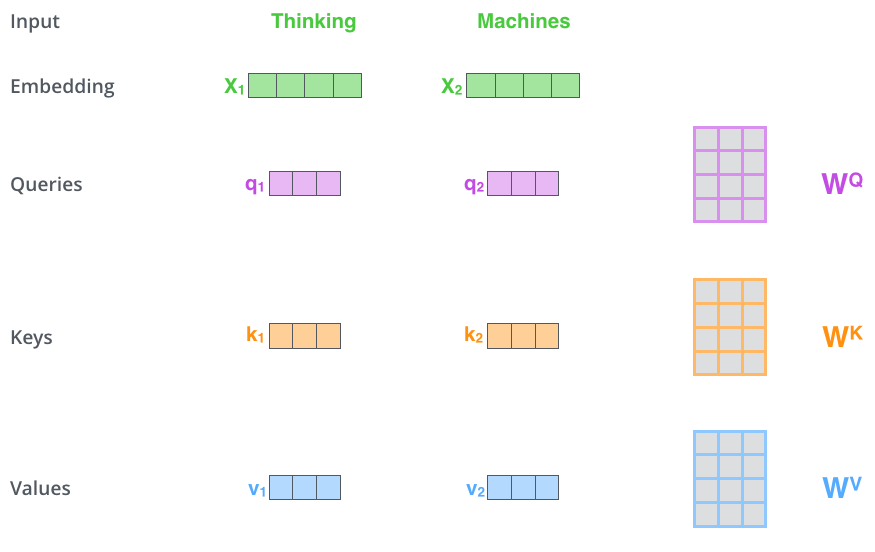
Self-attention step 1: create Query vector, Key vector, and Value vector [1]

第二步：计算自注意力分数。 如下图所示，计算分数时，对于任意一个词向量，用该向量对应的$q$与整个序列中所有$k$进行点乘，并得到对应分数，这里将这个分数命名为‘自注意力分数’。例如，对于$X_1$，用其对应的$q_1$分别与该序列中$k_1$和$k_2$相乘，则得到$q_1\cdot k_1 = 112$， $q_1 \cdot k_2 = 96$。得到的这两个分数为标量，可以用来表示当前Query对应的token与其他所有tokens之间的关系，且分值越大，表示关系越强烈。可以看到，$q_1$与$k_1$点乘的数值比$q_1$与$k_2$点乘的数值更大。这个结果与我们的认知相符合，表明在一句话中，单词Thinking和它自己的关系比Thinking和Machines之间的关系更紧密。

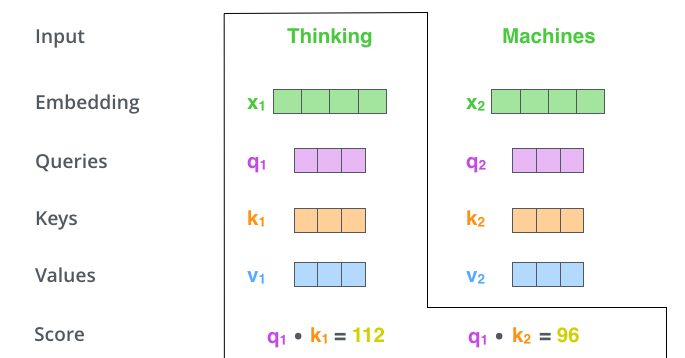
Self-attention step 2：calculating a self-attention score [1]

第三步和第四步的计算过程如下图所示。

第三步：调整自注意力分数幅值。 调整上一步自注意力分数幅值的目的是使神经网络训练更加稳定，这在一些迭代优化算法中是经常使用的操作。在实际训练中，如果q和k计算得到的自注意力分数幅值过大，则在进行softmax操作时会导致梯度极小，很容易出现梯度消失现象（其原因很好理解，结合softmax函数曲线可以看到，如果自注意力分数幅值过大，则会分布在softmax函数两侧距离原点很远的位置，而这些位置的梯度极小）[3]。为了解决上述问题，一种常见的算法是给第二步得到的score除以$\sqrt{d_{k}}$，其中$d_k$表示向量$k$的维度。图中$d_k$的数值为256，因此$\sqrt{d_{k}}$的数值为8。

第四步：softmax。 将上一步的得到的自注意力分数进行softmax操作，使得所有分数都为正数，且所有分数之和为1。

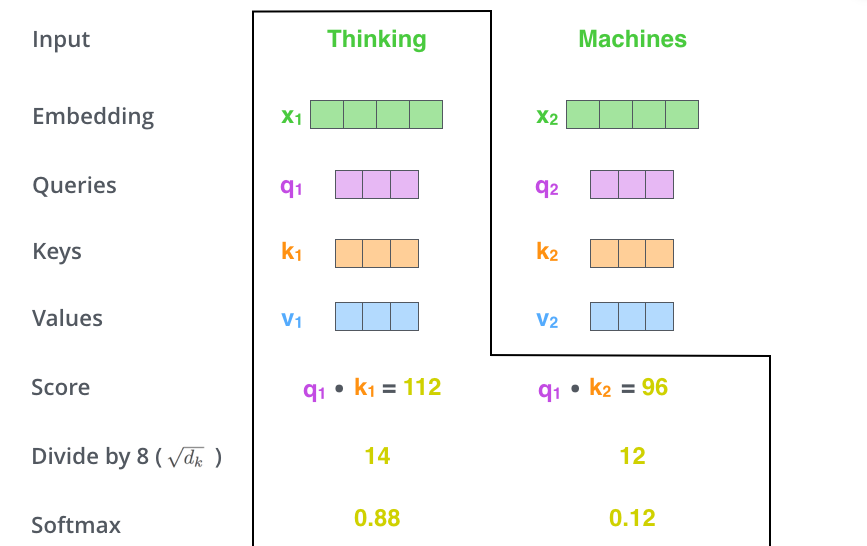
Self-attention step 3-4：divide the scores and softmax. [1]

第五步和第六步的计算过程如下图所示。

第五步：将第四步中经过softmax之后的分数与对应的Value（$v$）相乘。 这一步操作的目的是希望通过score的数值来保持序列中想要关注（相关）单词的权重，同时降低不相关单词的权重。

第六步：将第五步中加权之后的所有Values值相加，并生成新向量Z。 例如，对于第一个单词Thinking，将前五步计算的最终结果$v_1$和$v_2$相加，得到$z_1$；同理，$z_2$也通过相同方式得到单词Machines对应的输出结果。

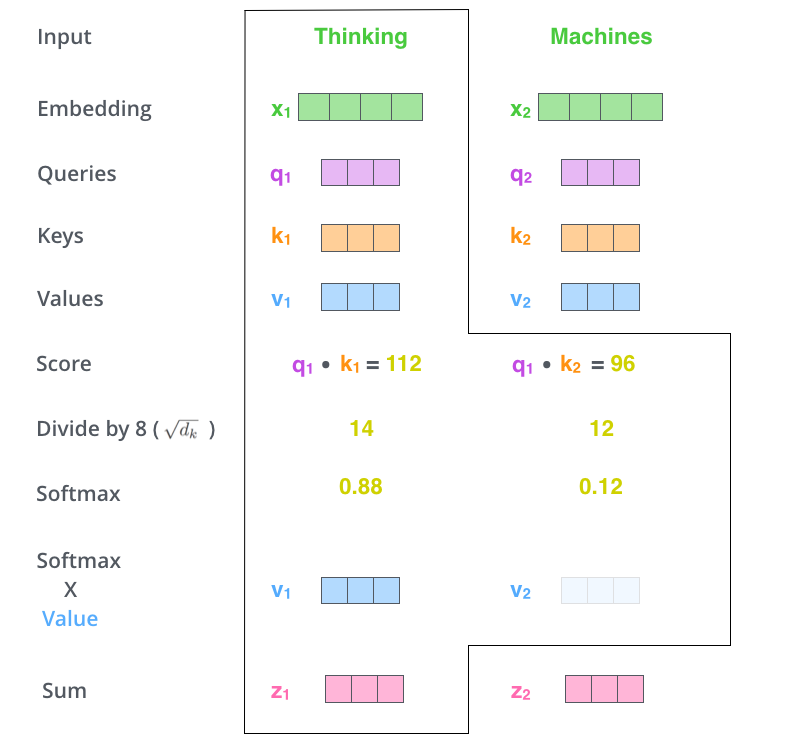
Self-attention step 5-6. Step 5: multiply each value vector by the softmax score. Step 6: sum up the weighted value vectors [1]

至此，我们介绍完了自注意力机制的计算过程及其设计目的。用一句话总结一下，self-attention的过程就是通过query和key进行相乘计算出一个关系权重，再采用这个关系权重对value进行加权求和，以提升一个序列中相关元素的权重，降低不相关元素的权重。

为提升计算效率，上述自注意力过程在实际操作中一般通过矩阵表达进行并行计算。接下来，将介绍自注意力机制的矩阵表达。

矩阵表达

如下图所示，在矩阵表达中，首先将一个句子序列中所有单词的编码结果叠加为一个二维向量$X$，$X$中每一行表示一个单词。一个序列中每个单词对应的q, k, v可以直接通过一次矩阵相乘计算得到，这里用大写字母Q，K和V表示。类似地，Q, K, V中每一行代表一个单词对应的q, k, v。

Self-attention matrix 1 [1]

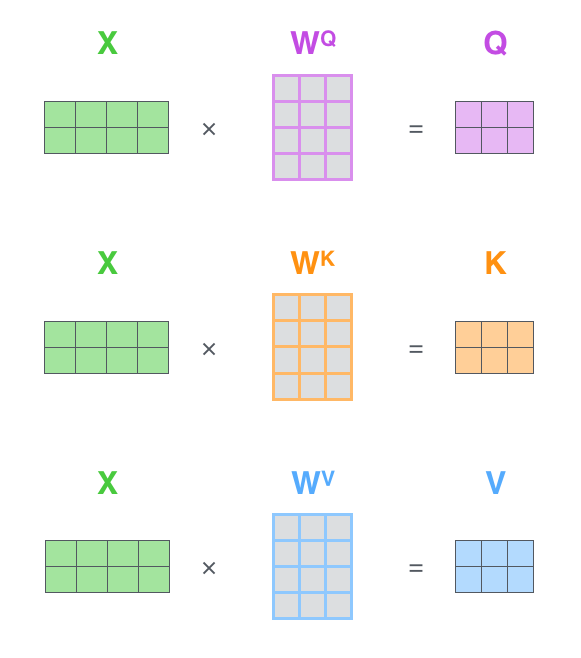
接下来，将自注意力中所有其余计算步骤结合在一起，如下图所示。首先，计算$QK^{T}$,；然后将结果除以$\sqrt{k_{k}}$并进行softmax操作；最后，将计算结果与V相乘，得到输出结果Z。这里Z中每一行表示一个单词对应的自注意力输出结果。

Self-attention matrix 2 [1]

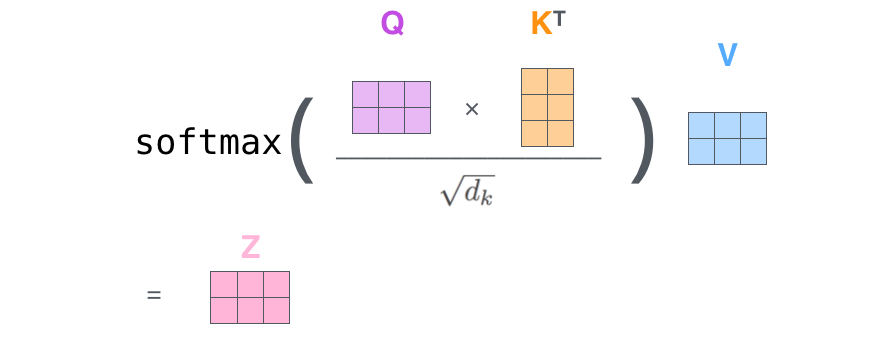
至此，我们介绍完了自注意力机制的矩阵表达。

数学表达

根据自注意力机制矩阵表达的最后一个图，可以写出自注意力机制的数学表达如下：

\[\tag{1} \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V\]

这里Q, K, V分表表示矩阵形式的query，key和value；$d_{k}$表示向量key的维度。

下图是self-attention在Transformer[3]中的示意图，同样很好地总结了自注意力模型的计算过程。

Self-attention in Transformer [2].

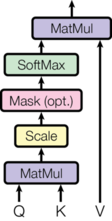
代码分析

注意力机制的代码如下所示:

def attention(query, key, value, mask=None, dropout=None):
    "Compute 'Scaled Dot Product Attention'"
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) \
             / math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = F.softmax(scores, dim = -1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn

上述代码结合公式（1）很容易理解，因此不做过多介绍，下面仅对变量的维度进行简要分析。

以Vision Transformer中的应用为例，令输入图像维度为[B, C, W, H]，其中B, C, W, H分别为batch size，特征图（或图像）通道数，特征图（或图像）宽度和高度。 由于Transformer仅支持序列为输入，因此一般需要将W和H维度合并，表示为WH。

根据上述信息，query（Q）的维度为[WH, B, C], key（K）的维度为[WH, B, C], K的转置维度为[WH, C, B], value（V）的维度为[WH, B, C]。

则$Q K^{T}$维度为[WH, B, B]，与V相乘后输出结果的维度为[WH, C, B]。可以看出，输出变量的维度和V的维度是相同的。

注: 通过$QK^{T}$的输出维度可以看到，$QK^{T}$的维度与C无关了，由于B仅为batch size，我们不必关心，因此Q和K相乘之后相当与在WH维度计算了一个注意力权重，用于和V相乘。这一点特别像CV中的空间注意力机制。

多头自注意力

相比于前文所述的自注意力，多头自注意力的优势可以总结为两点[1]：

（1）多头自注意力使得模型能够同时关注多个重点区域。在前序语言模型中，我们发现自注意力模型将自身计算为最值得关注的对象（当然，模型训练之后不一定如此），如果增加多个注意力头，就可能使模型关注一些除自己本身之外的对象。

（2）多头自注意力为模型的注意力层提供了多个表示子空间（representation subspaces）。多头自注意力中将有多个学习Q, K, V的权重矩阵，这些矩阵均是独立地随机初始化，然后将输入向量映射到不同子空间中，进而丰富了信息的特征表达。

接下来，我们首先通过一组图示来介绍多头自注意力的基本原理，然后给出其公式表达，最后对相应代码进行分析。

多头自注意力的过程和基本原理

由于前文介绍了自注意力机制的矩阵表达，因此这里直接采用矩阵形式对多头自注意力进行描述。

首先，如本节开始时所讲，多头自注意力需要单独学习多个Q, K, V矩阵，因此也就对应着多个学习Q, K, V的权重矩阵 $W_{i}^{Q}$, $W_{i}^{K}$ 和 $W_{i}^{V}$，输入矩阵X与对应的权重矩阵$W_i$相乘，得到对应的Q, K, V。该过程如下图所示（图中展示了两个头的自注意力，因此有两组独立的Q, K, V）。

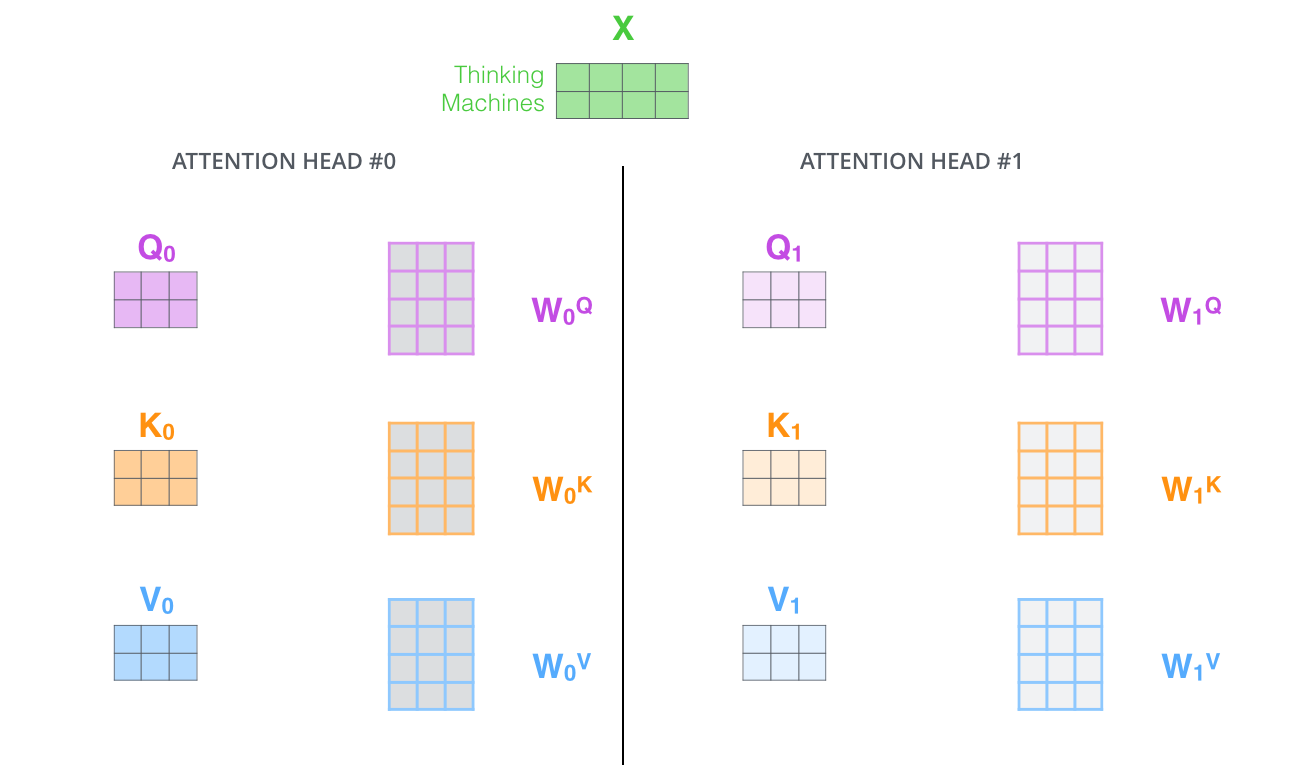
Multi-Heads self-attention: learn Q, K, V. [1]

然后，根据前续自注意力一节的内容，分别对每个注意力头单独计算自注意力，并得到对应输出$Z_i$。假设有8个注意力头，则会得到8个对应的输出$Z_0$~$Z_7$，如下图所示：

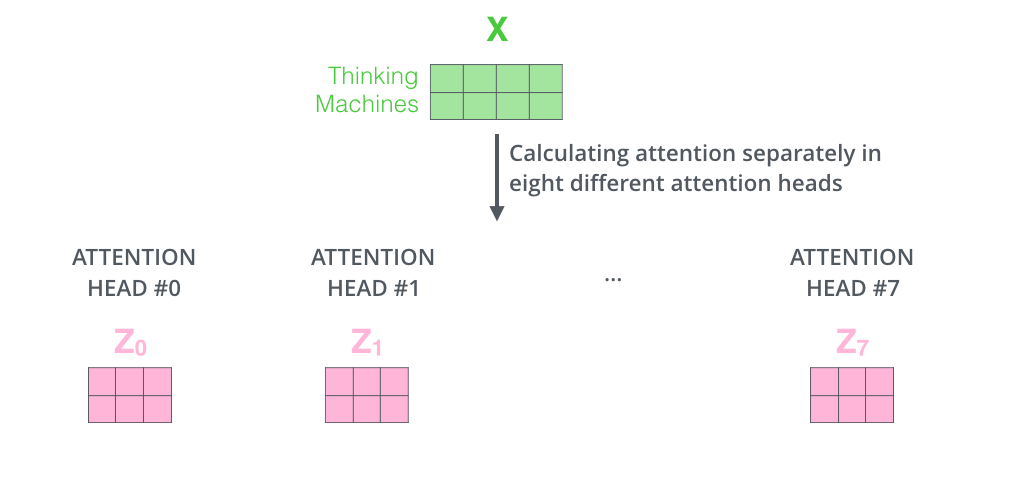
Multi-Heads self-attention: calculate self-attention separately. [1]

显然，上一步得到的多个输出$Z_i$不能直接用于全连接层的输入，因此需要将多个输出整合为一个矩阵再输出。

为此，多头自注意力的做法是先将所有的$Z_i$拼接为一个整体，然后再乘以一个输出矩阵$W^{O}$，该过程如下图所示：

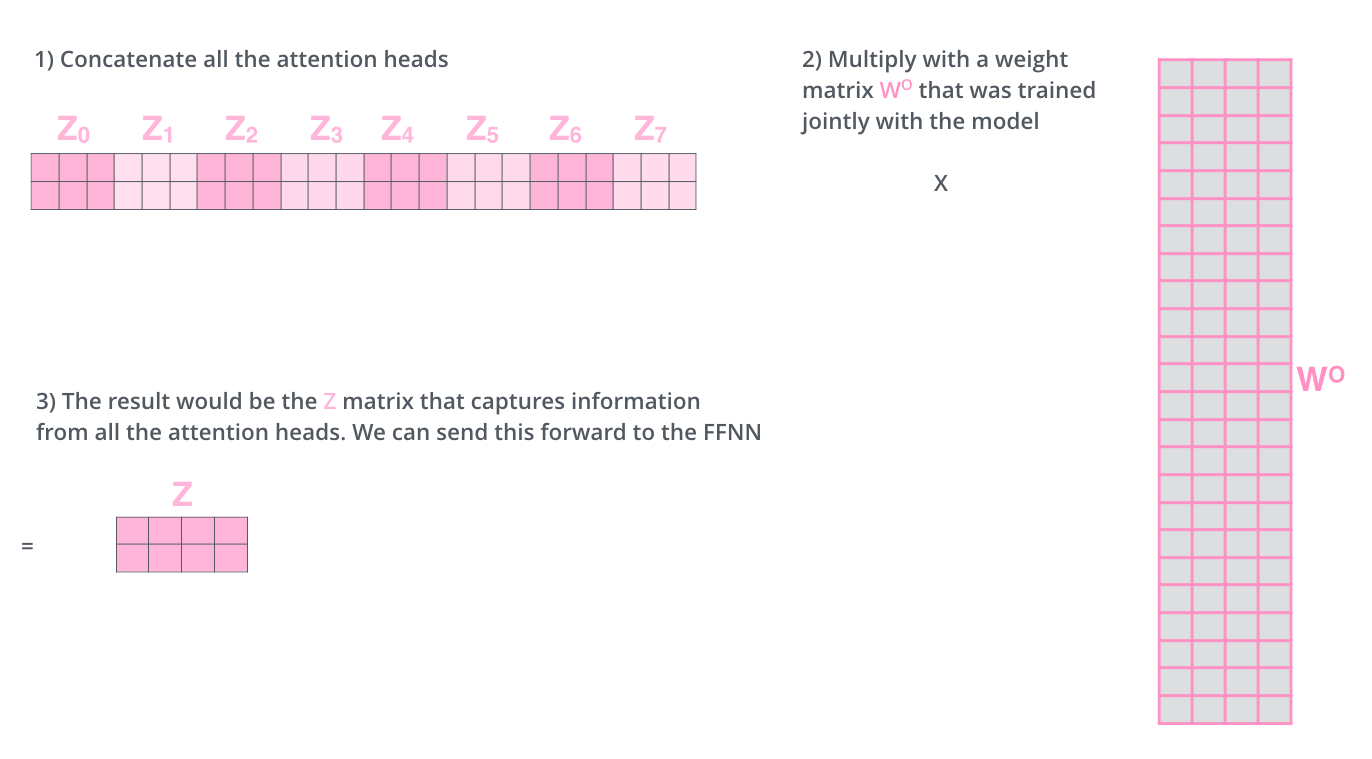
Multi-Heads self-attention: concat and multiply a output matrix. [1]

最后，将多头自注意力机制的整个流程总结为一幅图，如下：

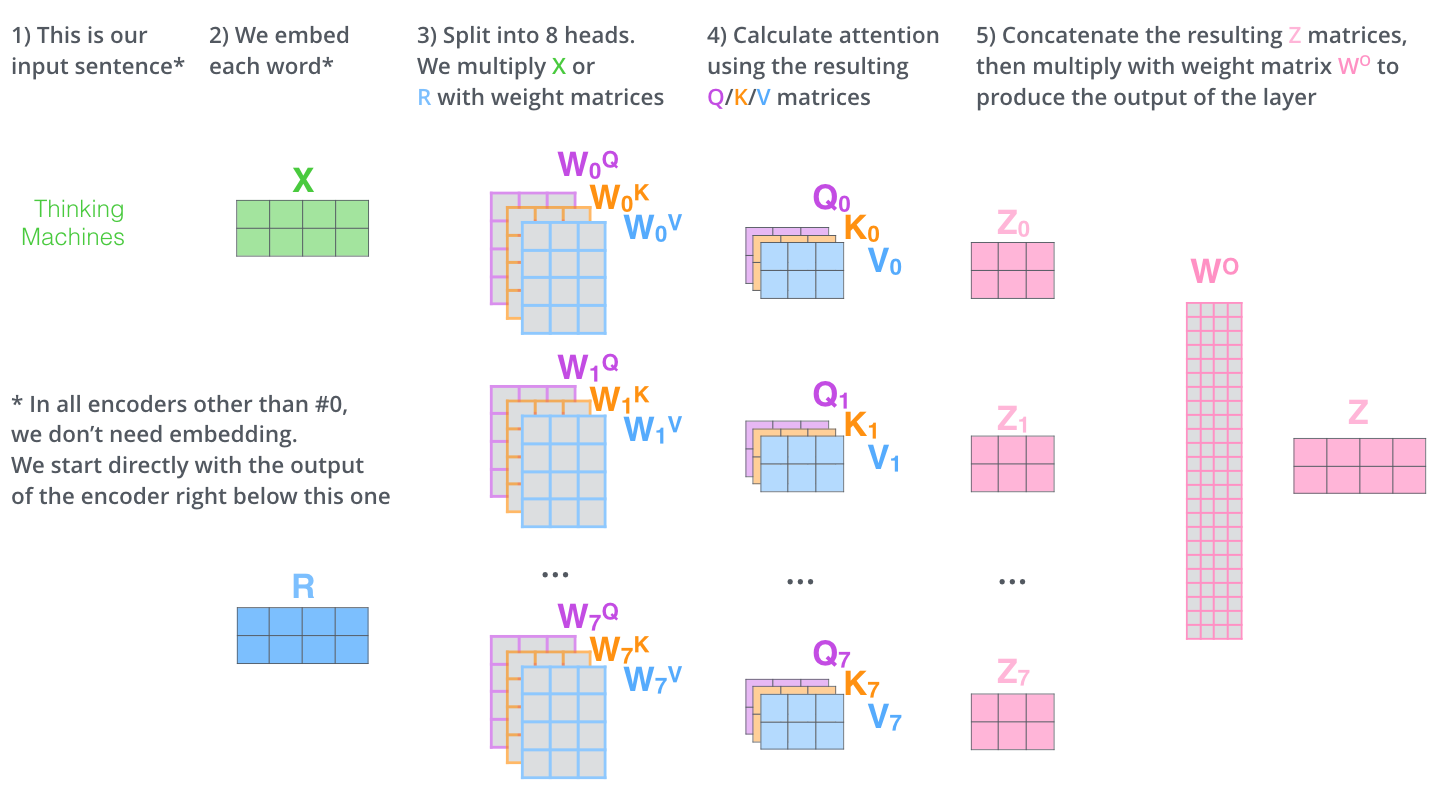
Multi-Heads self-attention: overview. [1]

至此，我们介绍完了多头自注意力模型的计算流程及其设计目的。以句子翻译为例，如下图，当注意力存在多个头时，一个头将单词it的注意力集中到The animal，另一个头将注意力集中到tired，可见增加了注意力模型的表达能力。当然，若注意力头继续增加，可能会出现一些无法用直观进行解释的现象，但这并不影响多头自注意力优越的性能。

Visualization 1 [1]

数学表达

结合基本原理，多头自注意力的数学表达如下[3]：

\[\tag{2} \mathrm{MultiHead}(Q, K, V) = \mathrm{Concat}(\mathrm{head_1}, ..., \mathrm{head_h})W^O \\ \text{where}~\mathrm{head_i} = \mathrm{Attention}(QW^Q_i, KW^K_i, VW^V_i)\]

其中，$W^Q_i \in \mathbb{R}^{d_{\text{model}}\times d_k}$, $W^K_i \in \mathbb{R}^{d_{\text{model}}\times d_k}$, $W^V_i \in \mathbb{R}^{d_{\text{model}} \times d_v}$，$W^O \in \mathbb{R}^{hd_v \times d_{\text{model}}}$，$d_{model}$表示序列编码长度。一般地，自注意力头数设置为8，即$h=8$，而$d_k=d_v=d_{model}/h$。

下图是multi-heads self-attention在Transformer[3]中给出的示意图，总结了多头自注意力模型的计算过程。可以看出，该图能够很好地对应多头自注意力模型的数学表达。

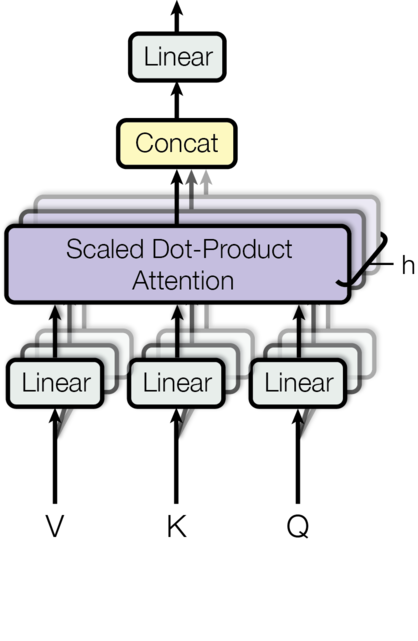
Multi-heads self-attention in Transformer [2].

代码分析

多头自注意力的代码如下所示:

def clones(module, N):
    "Produce N identical layers."
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        "Take in model size and number of heads."
        super(MultiHeadedAttention, self).__init__()
        assert d_model % h == 0
        # We assume d_v always equals d_k
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)
        
    def forward(self, query, key, value, mask=None):
        "Implements Figure 2"
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1)
        nbatches = query.size(0)
        
        # 1) Do all the linear projections in batch from d_model => h x d_k
        query, key, value = \
            [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
             for l, x in zip(self.linears, (query, key, value))]
        
        # 2) Apply attention on all the projected vectors in batch. 
        x, self.attn = attention(query, key, value, mask=mask, 
                                 dropout=self.dropout)
        
        # 3) "Concat" using a view and apply a final linear. 
        x = x.transpose(1, 2).contiguous() \
             .view(nbatches, -1, self.h * self.d_k)
        return self.linears[-1](x)

首先，对代码中几个关键点解释如下：

  1. 关于变量，h和d_module分别表示注意力头数和输入序列长度，d_k表示key的序列长度。

  2. self.linears = clones(nn.Linear(d_model, d_model), 4)一句话中定义了4个全连接层，这4个全连接层就对应了四个权重矩阵$W$，前三个矩阵用于学习Q, K, V, 最后一个权重矩阵$W$用于将拼接的多头注意力输出转化为一个输出矩阵。

  3. （这一条需要结合Transformer的整体结构理解）MultiHeadedAttention的forward函数中query, key, value第一次输入时，query和key一般为src+pos_embeding，而value直接设置为src即可（这样设置的原因是，在学习序列中加上位置信息有助于学习不同元素之间关系，而计算每个元素的新value时无需加上位置信息）。在第二次及以后，foward中的query, key和value直接使用上一层输出即可。

然后，继续以计算机视觉中Vision Transformer为例，理解多头自注意力中变量的维度变化。令输入图像的维度为[B, C, W, H]，其中B, C, W, H分别为batch size，特征图（或图像）通道数，特征图（或图像）宽度和高度。由于Transformer仅支持序列为输入，因此一般需要将W和H维度合并，表示为WH。则多头注意力机制可大致分为如下三个关键步骤：

第一步：根据上述信息，令Q, K, V的维度均为[B, WH, C]（注意，这里的维度顺序和上一节不同，因为后面多头注意力要多分出来一个维度。此外，这里Q, K, V还没有通过权重矩阵W，因此虽然名字是Q, K, V，但需要理解为输入向量）。通过如下代码，首先将Q, K, V分别输入权重矩阵（l(x)），然后将输出的维度改变为[B, WH, h, d_model//h]（view(nbatches, -1, self.h, self.d_k)，这里d_model等价于C），最后改变维度顺序为[B, h, WH, d_model//h]（transpose(1, 2)）。

# 1) Do all the linear projections in batch from d_model => h x d_k
query, key, value = \
    [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
        for l, x in zip(self.linears, (query, key, value))]

第二步：计算attention:

# 2) Apply attention on all the projected vectors in batch. 
x, self.attn = attention(query, key, value, mask=mask, 
                            dropout=self.dropout)

根据上一节的分析，输出变量x的维度和value的维度相同，即[B, h, WH, d_model//h]。

第三步：合并输出变量，然后通过一个权重矩阵并输出最终结果。首先将x的维度由[B, h, WH, d_moudel//h]变为[B, WH, h, d_model//h]（transpose(1, 2).contiguous()）；然后将x的维度转化为[B, WH, C]（view(nbatches, -1, self.h * self.d_k)）；最后，将结果通过权重矩阵W，维度不变（self.linears[-1](x)）。

# 3) "Concat" using a view and apply a final linear. 
x = x.transpose(1, 2).contiguous() \
        .view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x)

因此，最终输出结果的维度为[B, WH, C], 与输入保持一致。

注：类比计算机视觉方法，多头注意力机制中将C拆分为$h\times \textit{d_k}$的做法相当于在channel维度将特征图分组，然后每个组别计算一次attention，组内部的attention关注spatial信息。因此，多头注意力机制特别类似于计算机视觉中同时使用spatial和channel attention。当然，视觉中的attention机制是基于NLP中attention提出的。

计算复杂度分析

在Swin Transformer一文中[8]，作者给出多头注意力的计算复杂度为$\Omega(MSA)=4WHC^{2} + 2(WH)^{2}C$，本节分析下是怎么计算的[7]。

单头注意力

首先，忽略batch size的维度，令输入矩阵X的维度为[WH, C], 生成Q, K, V的矩阵矩阵分别为$W_Q$, $W_K$, $W_V$， 假设Q, K, V的channel数量与X一致，则有（为了方便显示矩阵维度，本节将权重矩阵中的Q, K, V角标放在下面了，和前文有些差别）：

\[X^{WH \times C} \cdot W_{Q}^{C \times C}=Q^{WH \times C}\] \[\tag{3} X^{WH \times C} \cdot W_{K}^{C \times C}=K^{WH \times C}\] \[X^{WH \times C} \cdot W_{V}^{C \times C}=V^{WH \times C}\]

公式（3）中生成Q, K, V过程的计算量为$3\cdot WHC^{2}$。

注：令矩阵A维度为[a, c]，矩阵B的维度为[c, b], 则A$\cdot$B的计算量为abc。

然后，计算$QK^{T}$，有：

\[\tag{4} Q^{WH\times C}\cdot K^{T(C\times WH)} = z^{WH\times WH}\]

公式（4）中的计算量为$(WH)^{2}C$。

Softmax操作以及除以$\sqrt{d_{k}}$计算量可以忽略不计，因此仅需计算最后的乘以V操作。令softmax操作之后的值为$\tilde{z}$，则：

\[\tag{5} \tilde{z}^{WH\times WH} \cdot V^{WH \times C} = Z^{WH \times C}\]

该过程（公式（5））的计算量为$(WH)^{2}C$。

综上所述，对于单头注意力模型，其总计算量为$3WHC^2+2(WH)^2C$。

多头注意力机制

相比于单头注意力，多头注意力的计算量仅多了最后一步中输出矩阵与拼接后输出的乘法，即：

\[\tag{6} Z^{WH\times C} \cdot W_{O}^{C\times C} = Z^{WH \times C}\]

该过程的计算量为$WHC^2$。

因此，多头注意力模型的总计算量为$4WHC^2+2(WH)^2C$。

总结

Transformer中自注意力在大量学习一种关系，即当前token和其他tokens之间的关联性，在数学上，上述这种关系就是通过$QK^T$计算而来，二者的计算结果为一个权重系数，再将权重系数与对所有对应的$V$进行加权求和，即可得到当前token的新特征。在一个序列中，即使两个tokens之间的距离非常远，只要它们被考虑在内，就会计算它们之间的关联（有点类似协方差矩阵中随机变量内部元素之间的相关性）。这也就是文献中经常说的Transformer对长依赖(long-range dependence)处理较好。这种对全局信息的掌控能力也正是CNN缺少的，因为CNN具有局部连接特性，虽然对局部信息的处理更具优势，但在全局信息的把握上却不够充分。同时，CNN的这种归纳偏置(inductive bias)限制了其在超大规模数据集上的性能。

当然，通过前文对计算复杂度分析可以看出，经典Transformer中的多头自注意力机制在图像上的计算复杂度为$4WHC^{2} + 2(WH)^{2}C$，这将限制Transformer在CV领域的推广，因为图像的维度要比文字序列高的多。后面，我们将介绍一种在CV中降低自注意力机制计算复杂度的策略。

最后，将Transformer中多头注意力模型和CV中的Attention模型进行类比，可以发现二者之间有一些关联之处。可以认为多头注意力模型就是在channel维度对特征进行了分组（每个头为一组），并对每个组分别进行spacial attention，最后再合并计算最终输出，这使得CV领域和NLP领域的Attention极为相似。当然，需要注意，CV领域的attention机制是受NLP领域self-attention启发而提出的，因此二者如此相似也就不难理解了。

参考文献

[1] The Illustrated Transformer

[2] The Annotated Transformer

[3] Vaswani et al. Attention Is All You Need, NIPS 2017

[4] DETR详解

[5] Hu et al. Squeeze-and-Excitation Networks, TPAMI, 2018

[6] MultiHeadAttention实现详解

[7] Swin-Transformer网络结构详解

[8] Z. Liu et al. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows, ICCV, 2021